
 | Современное программирование предлагает пользователям использовать самые разнообразные языки программирования. Но основой основ является Паскаль.Данный язык был разработан в 1971 году в Университете Цюриха профессором Никлаусом Виртом. Его предназначение изначально было учебным. Имея достаточно четко выраженную структуру и систему предоставления данных Паскаль имел ограничения в функциях ввода - вывода, при создании подпрограмм. |
|---|
Управляющие операторы языка |
|---|
|
Задание. Разработать программу, которая определяет корень непрерывной функции f(x) на заданном отрезке [a, b] методом хорд. Метод работает в том случае, если значения функции на концах отрезков разных знаков, то есть, если функция только касется оси абсцисс, то ее корень данным методом определить нельзя. Если на заданном отрезке у функции несколько корней, то используя данный метод, найдем один из них. Метод хорд заключается в следующем, значения функции на концах отрезка соединяют отрезком прямой. В точке пересечения этой прямой с осью абсцисс определяют значение функции. Если это значение меньше заданной погрешности функции, то абсцисса точки пересечения считается корнем функции, иначе корень функции ищется на том отрезке из двух полученых, для которого значения функции на концах разных знаков. Графическая интерпретация метода нахождения корня методом хорд 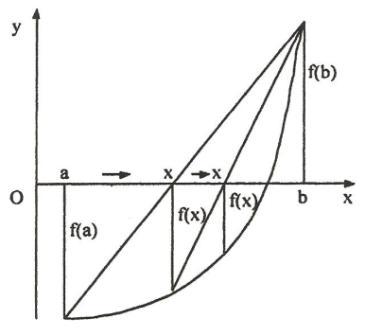
Схема алгоритма программы для функции f(x)=x2-1 
Полученный алгоритм является не структурным, так как цикл, который в нем использован не является ни циклом - до ни циклом - пока. Для преобразования алгоритма в структурный используем прием, рассмотренный ранее пример. А именно, повторяем в конце тела цикла операторы, выполняемый в начале цикла до условия и организуем цикл, как цикл - пока. Поскольку выход из цикла - пока осуществляется по нарушению условия цикла, придется также изменить условие цикла. Программа, реализующая стрктурный варинт алгоритма, имеет следующий вид: Program ex; Var a, b, f, fa, fb, eps, x:real; Begin WriteLn (`Введите a, b и эпсилон:`) ReadLn (a, b, eps); fa:=a*a-1; fb:=b*b-1; if fa*fb>=0 then WriteLn (`Метод не применим`) else begin x:=(b-a)*abs(fa)/abs(fa-fb)+a; f:=x*x-1: while abs(f)>=eps do {условие выхода из цикла} begin if fa*f<0 then begin b:=x; fb:=f; end else begin a:=x; fa:=f; end; x:=(b-a)*abs(fa)/abs(fa-fb)+a; f:=x*x-1 end; WriteLn (`При x=`, x:9:6, `y=`, f:10:8); end; End. Меняя значение погрешности, получим разные значения корня и значения функции в корне.
Зная точное значение корня x=1, определяем предельную, абсолютную и относительные погрешности в каждом случае. Из таблицы видно, что погрешность корня меньше погрешности значения функции. Однако, если бы производная функции в точке корня была близка к нулю, это соотношение было бы обратным, и следовательно, метод оказался бы неприменим. Соотношение Δy и Δx в зависимости от вида функции. 
В качестве альтернативы можно предложить алгоритм, в котором выход из цикла вычисленией выполняется когда разность между двумя соседними приближениями значений корня становится меньше заданного eps (по аналогии с примером). Однако, этот алгоритм был бы неприменим для поиска корня, если угол наклона производной функции в корне больше 45°. Следовательно, применяя тот или иной методы вычислительной математики, необходимо проверять обеспечение точности полученных результатов. |