Практическое занятие. Точность решения задач вычислительной математики. Вычисление определенного интеграла на заданном отрезке.

Современное программирование предлагает пользователям использовать самые разнообразные языки программирования. Но основой основ является Паскаль.Данный язык был разработан в 1971 году в Университете Цюриха профессором Никлаусом Виртом. Его предназначение изначально было учебным. Имея достаточно четко выраженную структуру и систему предоставления данных Паскаль имел ограничения в функциях ввода - вывода, при создании подпрограмм.

Управляющие операторы языка

Вычислительная математика занимается рассмотрением численных методов вычисления значения функций, решения алгебраических и трансцендентных уравнений, систем уравнений, интерполяции функции и т. д. К той же группе задач относится и задача о нахождении суммы ряда, рассмотренная в предыдущей статье. Попробуем на примере продемонстрировать проблемы достижения заданной точности результатов, которые возникают при решении задач этой области.

Задание. Разработать программу вычисления определенного интеграла функции f(x) на заданном отрезке [a,b] методом прямоугольников.

Определенный интеграл вычисляется как площадь фигуры, ограниченной графиком функции, отрезком оси абсцисс и вертикальными линиями, проходящими через границы отрезка. Метод прямоугольников предполагает, что площадь определяется как сумма площадей n прямоугольников, основанием которых является n-я часть отрезка [a, b], а стороной - значение функции на одном из концов отрезка (например левом, как на рисунке)

Вычисление определенного интеграла методом прямоугольника.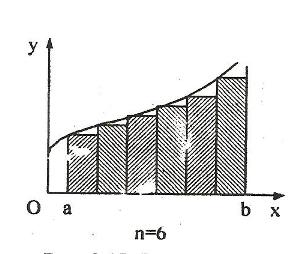

Итак, S1=f(x₁)*b+f(x₂)*b+f(x₃)*b+...f(x_n)*b=Eⁿ_i=1f(x_i),

где: b=(b-a)/n)

Значение определенного интеграла S1, определенное по данной формуле, является неточным, причем с увеличением количества отрезков, n-точность значения S1 увеличивается. Считают, что значение определено с заданной точностью, если абсолютная величина разности двух последовательных приближений результата, полученных при разных значениях n не превышает заданной точности.

Для определения момента достижения заданной точности необходимо организовать еще один внешний цикл, в котором значение n будем увеличивать, например в 2 раза, и рассчитывать значение S1, предварительно сохранив предыдущее значение S1 в переменной S2. Цикл должен завершаться когда абсолютная величина разности двух приближений S1 и S2 станет меньше е. Исходное значение S2 примем достаточно большим, чтобы цикл не завершился при первой проверке условия.

Схема алгоритма вычисления определенного интеграла для функции f(x)=x²-1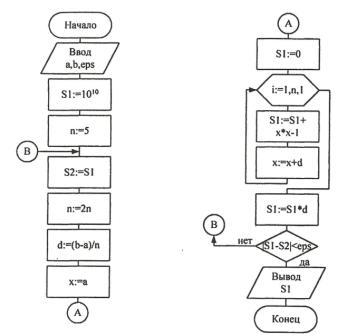

Программа, реализующая данную схему алгоритма:

Program ex;

Var a, b, S1, S2, d, eps, x:real; n, i:longint;

Begin

WriteLn (`Введите a, b и эпсилон:`);

ReadLn (a, b, eps);

S1:=1E+10;

n:=5;

repeat

S2:=S1;

n:=n*2;

d:=(b-a)/n;

x:=a;

S1:=0;

for i:=1 to n do

begin

S1:=S1+x*x-1;

x:=x+d;

end;

S1:=S1*d;

until abs(S1-S2)< eps;

WriteLn (`i=`, S1:10:6);

End.

При выполнении программы с разными значениями погрешности eps и отрезком [0, 2] получаем разные приближения результата i. (См. таблицу)

eps	n	i	^i	b_i, %
0.01	640	0.660420	0.006	0.9
0.001	5120	0.665885	0.0002	0.06
0.0001	40960	0.666569	0.00004	0.012

Точное значение определенного интеграла равно 2/3. Определим абсолютную и относительную погрешности результата. В данном случае, абсолютная погрешность результата всегда будет меньше eps, так как это определяется самим методом. Последнее верно не для любого метода.

Управляющие операторы языка